Although it may appear to be a counterintuitive statement, Japan’s “lost 20 years” was not necessarily a meaningless period of stagnation. In fact, these two difficult decades were a period when Japan fulfilled the two conditions needed for economic growth. Japan, and particularly Japanese companies, skillfully responded to the “lost 20 years” to produce two enormous benefits. First is an unprecedented progress in cutting costs, boosting efficiency, restructuring operations and holding down wages. Second is the globalization of Japan’s companies as they became citizens of the world. Once deflation fueled by a strong yen winds down, Japan will be positioned to capitalize on these two benefits gained from 20 years of hard work. I believe that Japanese companies will stage a dramatic recovery in earnings once the yen weakens to about ¥110 to the dollar. During the past two decades, Japan’s purchasing power parity fell from ¥200 to ¥100 in relation to the dollar. What this means is that Japan cut costs more than any other country in the world. Statistics show that Japan’s unit labor cost plummeted over the past 20 years. These lower expenses will make Japanese companies extremely competitive in the years ahead. In the past, many companies in Japan responded to a strong yen by adopting an extremely inward-looking stance. But this time, Japanese companies responded by making operations more global. Furthermore, despite the challenges of the past 20 years, Japanese companies took full advantage of their technological superiority. Many products incorporate high-tech materials, components and devices that are virtual “black boxes.” Japan was penalized with a strong yen for its success at becoming extremely competitive. But if the yen weakens to a level that matches its purchasing power parity (¥115 to the dollar in 2009), we should see a strong rebound in corporate earnings. Looking at the yen-dollar exchange rate, the yen’s appreciation that followed the 2008 Lehman shock is just now coming to an end. We now stand on the verge of a switch to a weaker yen as the U.S. economy recovers and the Fed starts raising interest rates. This may very well start a virtuous cycle as a weaker yen stops deflation, and the end of deflation allows Japan to increase its economic growth rate. Contents (1) The first benefit of deflation fueled by a strong yen: The elimination of Japan’s high-cost structure (2) The second benefit of deflation fueled by a strong yen: Globalization of companies and maintenance of technological superiority (3) Will the yen’s strength end? Will deflation end? (4) The demise of the hypothesis that “Japan is unique” and end of deflation

(1) The first benefit of deflation fueled by a strong yen:The elimination of Japan’s high-cost structure

Deflation with a strong yen made Japan stronger

There is no doubt that it was a painful 20 years for Japan. But I think we should call this period the “20 years of being put to the test” rather than the “lost 20 years.” Consequently, we should instead view this as a time when Japan, and particularly Japanese companies, passed this test with high marks and gained two valuable benefits. The first benefit was unprecedented progress in cost cutting, efficiency, restructuring, wage reductions and deregulation. The second benefit was the further globalization of Japanese companies, making them citizens of the world.

Elimination of Japan’s high-cost structure

A comparison of Japan in the early 1990s and today clearly reveals the benefits of cost cutting. We can see the difference by looking at a Daiwa Research Institute (DRI) report in 1993 concerning the relationship between deregulation and the elimination of price differentials between Japan and other countries. (At the time, I was working at DRI and was in charge of this report. For more information, please refer to This is How Deregulation Will Change the Business World, which was produced by DRI in 1993 and published by Nippon Jitsugyo.) In 1993, the yen staged a strong rally that took the exchange rate to ¥107 to the dollar. But purchasing power parity was ¥190 to the dollar, creating a price gap of about 100% with other countries. The objective of DRI was to use comparisons with other countries to determine the status and causes of Japan’s high prices. Finding a way to eliminate this price differential was the central theme. DRI planned to accomplish this by comparing the causes of price gaps for 21 major products with overseas cost structures. In 1993, Tokyo was the world’s most expensive city, as you can see in Figure 2. A study by 21 analysts of the causes of the price differential between Japan and other countries revealed three major factors. First was the unusually high cost of labor (denominated in dollars) because of the yen’s remarkable strength. Second was the high cost structure of Japanese companies (distribution expenses throughout the economy are high, resulting in high selling, general and administrative expenses and other indirect expenses for Japanese companies). Third was regulations in Japan and the widespread practice of companies to ignore efficiency (Figure 3). Consequently, the obvious prescription for Japan in response to the yen’s appreciation in 1993 was the following three actions: (1) absorb the high cost of labor by raising labor productivity; (2) restructure companies and boost efficiency, reform Japan’s merchandise distribution system; and (3) use deregulation and measures to promote competition to lower market prices. At that time, DRI, where I was working, the Japanese government, opinion leaders and the media all agreed that the above three initiatives were needed.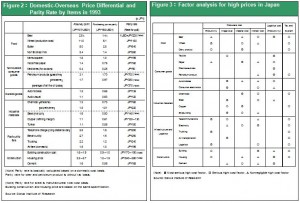

Japan’s high prices have been eliminated

Let’s look back on these three initiatives now that 18 years have gone by. Japan’s purchasing power parity, an indication of macroeconomic trends, has increased steadily. As I explained in my previous report, parity has climbed from ¥200 to the dollar in the early 1990s to ¥115 in 2009. This is a difference of almost 100% in relation to the dollar. Obviously, there has been a big improvement in Japan’s high prices and high-cost structure. Looking at individual items, the gap of 50% to more than 100% that existed between Japanese and U.S. utility rates in 1993 has disappeared. Moreover, Japan now has lower prices for airline tickets, subway tickets and telephone bills. The more than 100% difference in electricity rates is almost gone. For food products, the Japan-U.S. price differential was anywhere from two to 11 times in 1993. Wheat has dropped from 11 times to 30% and beer from 150% to 20%. Significantly, the price of a Big Mac, which is widely used as a benchmark for food price differences, is now 15% lower in Japan than in the U.S. (Washington D. C.). Even apparel is cheap compared with the U.S. thanks to UNIQLO and other low-price retailers (recent data for Japan are mainly from ‘International Price Levels (Comparison with Prices in Japan)’ by the Japan Center for International Finance, September 29, 2009).

The decline in the unit labor cost

So exactly how were these price reductions achieved? Let’s look at each of the three actions listed above. For action (1), Japan was highly successful at absorbing the high cost of labor by improving productivity and lowering wages. As Figure 4 shows, Japan raised productivity above the levels in other major countries while making big cuts in wages. The result was the only significant drop in unit labor cost among the world’s industrialized countries.

Remarkable progress in distribution system reforms

For action (2) as well, Japan has done extremely well. There have been substantial reductions in selling, general and administrative and other indirect expenses. Japan also made remarkable progress in improving how merchandise is distributed. Wholesalers and other intermediaries in the distribution system were eliminated. Symbolizing this progress was the rapid growth of a new business model called specialty store of private label apparel (SPA). U.S. retailer GAP was the first company to use this business model. But SPA really took hold in Japan. Until the late 1980s, manufacturers controlled Japan’s supply chain. Next, the manufacturer-wholesaler model, in which wholesalers are in control, took hold in the apparel industry. Today, the highly efficient UNIQLO-Nitori model (SPA, retailer-wholesaler), which controls upstream activities to achieve highly efficient distribution, is gaining momentum. UNIQLO is a retailer that is also involved in developing and manufacturing products. There are no intermediaries. Nitori, a retailer of furniture, interior goods and household products, uses the same framework. Companies using the Internet to sell products directly to customers are growing rapidly. Rakuten is an outstanding illustration. Another noteworthy trend in retailing is the emergence of convenience stores. These retailers captured a large share of the retailing market by greatly simplifying distribution channels. Consequently, Japan was able to achieve a big improvement in distribution efficiency thanks to the emergence of these three sources of distribution reforms: SPA, Internet sales and convenience stores.

Progress in deregulation, too

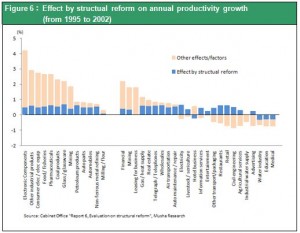
Japan has been making progress with deregulation and administrative reform, although more work remains. Deregulation and policies to encourage competition are responsible for the big reduction in the price gap in utility rates that I mentioned earlier. In its Structural Reform Evaluation Report 6 in December 2006, the Cabinet Office used indexes to show progress in deregulation covering all industries. As Figure 5 shows, the improvements were clearly evident. This report also includes an estimate of how much deregulation contributed to the improvement in productivity (Figure 6). Although this estimate may be too high, there is no doubt that reforms played a major role in raising productivity in sectors other than manufacturing.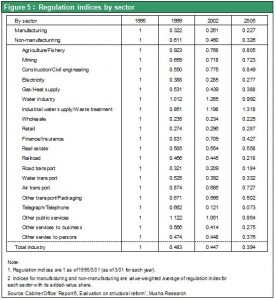

(2) The second benefit of deflation fueled by a strong yen:Globalization of companies and maintenance of technological superiority

The globalization of Japanese companies continues

My next subject is globalization, which is another way in which Japan benefited from 20 years of deflation linked to the yen’s strength. During this period, while rapidly making their operations more global, Japanese companies significantly raised overseas production ratios by making big overseas investments. Early in the 1990s, the theory that Japan is unique sparked a heated debate. People criticized Japan for producing highly competitive products at domestic factories while shutting out foreign investments. Japan was viewed as a fortress country that took away jobs by exporting massive quantities of these competitive goods and destroying industries in other countries. Table 7 shows that overseas factories accounted for less than 10% of production by Japanese companies at that time. This was far less than the overseas production ratios of the U.S. and European countries. By 2008, however, Japan’s overseas production ratio stood at 33%, which is about the same as in other major countries. Expanding overseas activities has enabled Japan to create rather than steal jobs in other countries. Japan’s overseas production ratio is estimated at more than 50% based on comparisons using the number of jobs, which is a more accurate reflection of production volume, instead of income (value added). At this point, Japanese companies have probably completed work on their global infrastructures. 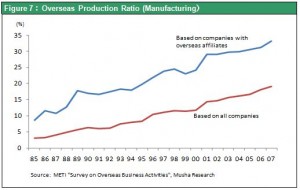As I have just explained, Japan made remarkable progress concerning two weaknesses that existed 20 years ago: a high-cost structure and a reclusive stance. Furthermore, while making these improvements, Japan still has a large number of products that are superior in terms of technology and quality (the emergence of companies in Korea and other countries has eroded Japan’s competitive edge in some product categories). Japanese companies preserved their superiority by giving priority to investments for developing technologies. This was done even while companies greatly reduced unit labor costs during the difficult period of deflation and a strong yen.

Technological superiority gives Japan a big advantage in new high-tech fields

The superiority of technologies and quality at Japanese manufacturers is most evident in high-tech components, materials and devices. Companies in Japan are not the most competitive suppliers of high-tech finished products like LCD televisions, cell phones and computers. But Japan has an overwhelming lead in supplying components and materials, which incorporate even more valuable key technologies. There are many examples: silicon, glass and back sheets for solar cells, semiconductor encapsulation materials, lithium-ion batteries for electric and hybrid automobiles, photoresist used to fabricate semiconductors, motors, and electronic components. Showa Shell Sekiyu has started making solar cells. Tokuyama, Shin-Etsu Chemical, SUMCO, Japan Solar Silicon and other companies have all announced plans to increase output of silicon for solar cells. Only Japan is able to produce high-tech materials, components and devices originating from semiconductor technologies entirely at domestic factories. Synergies resulting from this strength give Japan a valuable competitive advantage. Standardizing production processes for solar cells and lithium-ion batteries is difficult because technologies in these two fields are still in a relatively early stage of development. This prevents latecomer countries to the high-tech sector, from catching up for the time being. Consequently, Japan is very likely to retain its technological superiority. Japan also has a big competitive edge in the field of environmental products using technologies derived from semiconductors and other sophisticated devices. For example, Japan has a virtual monopoly in the supply of pure water systems, reverse osmosis membranes for desalinization, waste water recycling systems and other water treatment equipment, and carbon fiber used to make wind turbine blades. Infrastructure projects are another illustration of Japan’s superiority. Vietnam’s decision to use Japan’s high-speed rail technology is one example. In addition, Japan has considerable expertise in nuclear power, which is attracting renewed attention as a source of clean energy.

Japan excels at innovation centered on people

The superiority of products made by Japanese manufacturers is easy to see. In recent years, this same commitment to quality has become increasingly evident in sectors other than manufacturing, too. Until recently, the non-manufacturing and consumer products sectors in Japan were regarded as targeting only domestic demand. Companies in these sectors did not compete overseas. But Japan’s qualitative advantage in these two sectors will become increasingly evident in the years ahead. Personal income is climbing rapidly in emerging countries, particularly in Asia. Japan’s reputation for quality should enable Japanese companies to sell products at prices that include a quality premium. Japanese companies, both manufacturers and others, have proven expertise in innovation centered on people. Examples of hit products include the Wii (Nintendo), Suica smart prepaid cards (JR) and HeatTech clothing (Fast Retailing). Japan’s tourism industry will probably be another beneficiary of the country’s reputation for high-quality services. The number of tourists is likely to grow rapidly along with the rising number of affluent people in Asia. This is particularly true for Chinese tourists, who no longer need a visa to visit Japan.

(3) Will the yen’s strength end? Will deflation end?

Benefits of the end of the strong yen will emerge at once and generate strong earnings growth

As I have just explained, Japan’s “lost 20 years” was actually a time of progress. This was a period when Japan truly adapted to economic globalization by becoming a global citizen. Progress was made in cost-cutting and business operations, although more actions involving deregulation and administrative reforms are needed. This was also a period when Japan established a strong foundation for future growth. Once deflation linked to a strong yen reaches its end, I expect to see a strong surge in corporate earnings. This depends on the strength of the yen. The next crucial question is therefore if and when the yen’s appreciation will end.

What are the forces that determine exchange rates?

From a practical standpoint, foreign exchange rates should depend on either of two factors: (1) purchasing power parity (differences in rates of inflation) and (2) differences in interest rates. Differences in rates of inflation have an immediate impact on the cost-competitiveness of traded goods. The resulting change in trade (current account) surpluses and deficits raises or lowers demand for specific currencies. Figure 9 shows exchange rate movements for major countries with mature economies. As you can see, the rates generally stay within about 30% of the purchasing power parity. Over the long term, currencies do not move far from their purchasing power parities. Exchange rates do not precisely follow purchasing power parity mainly because of differences in interest rates. Interest rate gaps between countries chiefly reflect differences in economic strength. Since these gaps affect the capital account balance, the influence of interest rates is limited mostly to short-term changes in the supply and demand of currencies.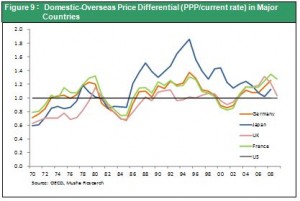

The unusual penalty imposed on Japan by a strong yen

Although foreign exchange rates should reflect purchasing power parity or interest rates, neither of these factors explains the unusual and prolonged strength of the yen that began in the 1990s. There were sharp increases in the yen’s value against the dollar in the late 1980s and around 1994. Both times, nominal and real interest rates in Japan were not particularly high in relation to U.S. interest rates. An upturn in the yen’s value was not needed from the standpoint of an interest rate gap. Furthermore, purchasing power parity of the yen was low at almost ¥200 to the dollar and the difference between the two countries’ inflation rates was minimal. Nowhere is there a reason to justify the yen’s climb to less than ¥100 to the dollar. The conclusion is that the yen’s appreciation that started in the 1990s was an extremely unusual phenomenon. We can even call this a penalty imposed on Japan. In the early 1990s, Japan had a huge trade surplus because of its overwhelming competitive strength and destructive effect on neighboring countries. We can say that the yen appreciated for the purpose of ending this situation. Japan became very competitive for a number of reasons. First is Japan’s free ride in the early postwar years owing in large part to generous U.S. technology sharing and U.S. markets that were open to imports. Second is the long period when the exchange rate was fixed at ¥360 to the dollar. This kept the yen at a level that was far below its purchasing power parity. Third is Japan’s closed markets. Overall, Japan’s competitive edge was a gift from a special environment created by these three factors along with other causes. From the standpoint of long-term economic rationality, an unusual increase in the yen’s value was inevitable to even things up after a free lunch.

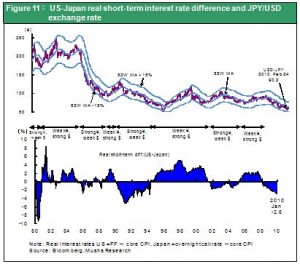
The interest rate gap has pushed the yen higher since 2008

The enormous gap between prices in Japan and other countries (costs rising faster than dollar-denominated export prices) has finally been eliminated. Based on the 2009 GDP, purchasing power parity is ¥115 to the dollar, which is not far from the current exchange rate. In addition, the emergence of economies in Korea, China and other countries means that Japan no longer has an overwhelming competitive lead. Japan’s trade surplus has dropped considerably. Although there is still a current account surplus, this surplus is negligible in relation to the surplus in China. For more than 15 years, Japan has paid the price for its free ride in earlier years. Japan no longer needs to suffer the effects of a currency that is stronger than its purchasing power parity. At last, the yen can return to a normal exchange rate that is within 30% of purchasing power parity just as for the world’s other major currencies. Taking these factors into consideration leads to the conclusion that the yen’s rise from ¥110 in late 2008 to as high as ¥85 versus the dollar (30% above its purchasing power parity) was not another penalty for Japan. This time, the yen appreciated because of the difference in interest rates as the U.S. cut interest rates to almost nothing to combat the Great Recession. If this is true, we can expect to see a reversal of the yen once the U.S. economy starts recovering and interest rates rise. There has already been a hike in the U.S. discount rate and officials are talking about a strategy for ending the emergency monetary easing measures. All these developments indicate that the peak of the yen’s appreciation is now behind us.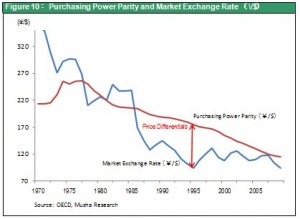

Never forget the tendency of exchange rates to be a self-fulfilling prophesy

Investors must keep in mind the tendency for exchange rates to be a self-fulfilling prophesy by spiraling in the same direction. Once the yen starts rising or falling, this movement itself becomes a cause for the exchange rate to continue moving in the same direction while gaining momentum. The result is a negative cycle in either direction. A stronger yen triggers deflation, which raises real interest rates and makes the yen even stronger. A weaker yen triggers inflation, which lowers real interest rates and makes the yen even weaker. These cycles are an undesirable phenomenon because they block the sustainability of economic growth by exaggerating exchange rate movements. Preventing this problem requires a suitable amount of intervention in foreign exchange markets. Furthermore, a decline in the yen to an appropriate level near its purchasing power parity (¥115 to the dollar in 2009) is just what the Japanese economy needs right now. Exchange rate and monetary initiatives will be required to accomplish this.

(4) The demise of the hypothesis that “Japan is unique” and end of deflation

The demise of the hypothesis that Japan is unique

Looking back, Japan’s problems probably originated in the early 1990s when people started speculating about whether or not Japan is unique. By the end of the 1980s, everyone in the world could see that Japanese manufacturers were so competitive that they had a destructive influence on the global economy. Japan was faced with two choices. One was to enact reforms to prevent negative impacts from this overwhelming competitive strength. For example, Japan needed to create jobs overseas and open its markets to imports. The other choice was to become less competitive. Enduring an extreme increase in the value of the yen was the price Japan had to pay to limit its competitiveness. As the yen appreciated, deflationary forces mounted. The result was a long period of stagnation that is now called “lost 20 years.” This is precisely the point that I discussed in Key Strategy Issue No. 287. Today, there is no doubt that Japan is not unique any longer.

Emergence of the view that China is unique

Now we are starting to hear people say that China is unique. Fears about China gaining a destructive power over nearby countries in the near future are greater than the fears about Japan in the late 1980s. China’s GDP (4.8 trillion) was about the same as Japan’s in 2009 and about one-third of the U.S. GDP. At the current growth rate, China’s GDP is likely to match the U.S. GDP within 10 years. Assuming nominal growth rates of 5% in the U.S. and 15% in China, the U.S. economy will expand by 27% over the next five years while China’s economy doubles. Even if the yuan’s value rises by 50%, China’s nominal GDP will be very close to the U.S. GDP after about five years. Furthermore, growth in foreign reserves means that China’s buying power is certain to become much greater than any other country. Looking at the current status of China’s free-market economy, democracy, commitment to the rule of law, property rights and intellectual property rights, this powerful economic presence will undoubtedly be a disruptive influence for the entire world. We must also remember that, even more than in Japan, China’s strength is derived from a growth structure that relies on other countries for technology, capital, markets and other items. This is why China’s present situation looks very much like a free ride. China must be held back and pressure applied to undergo a transformation from within. Accomplishing this demands an increase in the presence of nearby Japan in order to achieve a better balance with China. As a result, the need to exert pressure on China makes the possibility of a return of a penalty yen appreciation even smaller.

A prosperous decade for Japan after the end of deflation

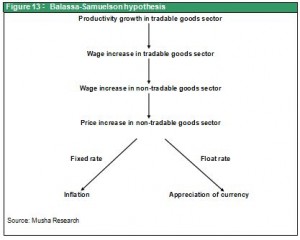
I believe that a positive cycle based on the Balassa-Samuelson hypothesis will begin once we reach the end of this increase in the yen’s value. In other words, we will finally see higher wages supported by strong productivity growth in Japan, too. This will quickly lead to wage increases in Japan’s non-manufacturing sectors, which will create inflation in the cost of services. The result will be nominal economic growth. Higher wages will contribute to more consumption that will make the economic growth rate even stronger. This is exactly the same principle for the deflation linked to the yen’s appreciation that took place during the “lost 20 years.” But this time, the principle is having the opposite effect. In this environment, we should expect to see a reappearance of inflation fueled by differences in productivity growth rates. With this type of inflation, wages and earnings can climb even in internal demand-based service industries where productivity is not improving. From the standpoint of starting this type of virtuous cycle as well, Japan must enact decisive reflation initiatives so the country can avoid the negative cycle of a stronger yen and deflation.